All content here is for research and educational purposes only, not financial advice.

Risk Analysis of a Naked Put Strategy with VRP>0 signal

In the previous part, we examined how there is opportunity to monetise VRP of AAPL using a simple VRP>0 signal. The simplest approach to it was to trade short puts and exit at around the half-life (~ 4 days)of the VRP decay process. While this simple strategy was found to be profitable and regime-resilient, the residual risks had not been assessed.

For naked puts, the downside risks can be hefty, and one extreme event could wipe out the many small wins from this strategy, or worse, multiple of such events could even result in an overall loss. It is therefore important to analyse the corresponding risks of this strategy, and implement hedges against them.

Examining the Tail Risks

We first examine the empirical distribution of the PnL to assess the magnitude and asymmetry of the tail risk associated with this strategy.

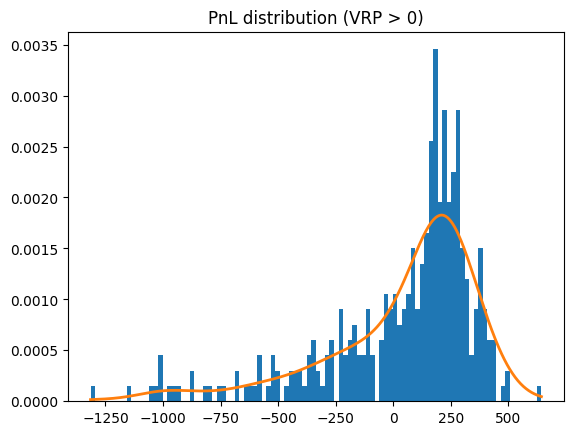
Table 1: Summary Statistics of PnL

Metric	Value
Number of trades	341
Mean PnL	40.45
Median PnL	160.00
Standard deviation	332.92
Maximum PnL	643.50
Minimum PnL	-1,315.00
Skewness	-1.53
Excess kurtosis	2.30
Tail dominance (worst 5%)	0.31

The distribution deviates substantially from normality, evidenced by its negative skewness (−1.53) and excess kurtosis (2.30), indicating asymmetric downside risk and fat-tailed loss behaviour.

Table 2: VaR and ES at 95% and 99% Confidence Levels

Risk Metric	95% Level	99% Level
Value-at-Risk (VaR)	-677.85	-1025.91
Expected Shortfall (ES)	-938.38	-1139.38

Given the VaR estimates, the strategy’s losses are observed to not exceed USD 677.85 and USD 1,025.91 at the 95% and 99% confidence levels, respectively. Of note, the VaR estimates are computed on a per-trade basis given the strategy’s trading approach. With the ES estimates, we can also observe average losses of USD 938.38 and USD 1139.38 conditional on the losses exceeding the respective VaR thresholds.

Nonetheless, while VaR and ES provide a measure of the extent of the risk, they do not explain the underlying causes for it.

Understanding Greeks-associated Risks Through Ito’s Formula

Given an options-based strategy, it is necessary to analyse the option Greeks and their associated risks, which govern both expected returns and tail-loss behaviour.

Deriving the Delta–Gamma–Theta PnL approximation from Itō’s formula

Let the option price be $V = V(S,t)$, where $S$ is the underlying price and $t$ is time. Assume the underlying follows a diffusion process:

\[dS = \mu S\ dt + \sigma S\ dW\]

1) Apply Itō’s formula

We consider the option value $V(S,t)$.

Itō’s formula gives:

\[dV = \frac{\partial V}{\partial t}\ dt + \frac{\partial V}{\partial S}\ dS + \frac{1}{2}\frac{\partial^2 V}{\partial S^2}\ (dS)^2\]

Define the Greeks:

\[\Theta := \frac{\partial V}{\partial t} \qquad \Delta := \frac{\partial V}{\partial S} \qquad \Gamma := \frac{\partial^2 V}{\partial S^2}\]

So:

\[dV = \Theta\ dt + \Delta\ dS + \frac{1}{2}\Gamma (dS)^2\]

2) Compute $(dS)^2$

Substitute $dS = \mu S\ dt + \sigma S\ dW$:

\[(dS)^2 = (\mu S\ dt + \sigma S\ dW)^2\]

Expand:

\[(dS)^2 = \mu^2 S^2 (dt)^2 + 2\mu\sigma S^2\ dt\ dW + \sigma^2 S^2 (dW)^2\]

Use the Itō multiplication rules:

$(dt)^2 = 0$
$dt\ dW = 0$
$(dW)^2 = dt$

Therefore:

\[(dS)^2 = \sigma^2 S^2\ dt\]

3) Substitute back into Itō’s formula

\[dV = \Theta\ dt + \Delta\ dS + \frac{1}{2}\Gamma \sigma^2 S^2\ dt\]

So the option’s instantaneous change decomposes as:

\[\boxed{ dV = \Delta\ dS + \left(\Theta + \frac{1}{2}\Gamma \sigma^2 S^2\right)dt }\]

4) Discrete-time approximation (PnL attribution form)

Over a short interval $\Delta t$, replace differentials with finite changes:

\[dV \approx \Delta V \qquad dS \approx \Delta S \qquad dt \approx \Delta t\]

This gives the familiar PnL approximation:

\[\boxed{ \Delta V \approx \Delta\ \cdot \Delta S + \frac{1}{2}\Gamma(\Delta S)^2 + \Theta\ \Delta t }\]

Note: In continuous time, the gamma contribution appears as $\frac{1}{2}\Gamma\sigma^2 S^2 dt$ because $(dS)^2$ collapses to $dt$. In discrete realised PnL attribution, it is written as $\frac{1}{2}\Gamma(\Delta S)^2$.

Interpreting the Itō Decomposition of PnL

The Itō decomposition above provides a direct mapping between option Greeks and realised PnL dynamics. Each term corresponds to a distinct risk channel that manifests differently in expected returns versus tail losses:

The delta term $\Delta \cdot \Delta S$ captures first-order directional exposure to movements in the underlying price.
The gamma term $\frac{1}{2}\Gamma(\Delta S)^2$ captures second-order convexity, causing losses to accelerate non-linearly during large price moves.
The theta term $\Theta\ \cdot \Delta t$ represents time decay, contributing positively to expected PnL for short option positions.

While theta contributes steadily to average returns, the quadratic scaling of the gamma term is a key driver of realised losses during sharp market declines. This asymmetry between linear income accrual and convex downside exposure underpins the risk profile of this short put strategy and motivates the focus on delta and gamma risks in the analysis that follows.

Qualitative Description of Greeks-Associated Risks

Table 3: Overview of Greeks-associated Risks

Risk	How it Affects Strategy’s PnL	What this Greek Means?
Theta	Income accrual	Rate of change of option price given time decay
Delta	Directional loss	Rate of change of option price given change in underlying price
Gamma	Tail amplification	Rate of change of Delta given a change in underlying price

As a strategy built on monetising VRP, vega exposure primarily drives expected returns and is secondary to delta and gamma in driving extreme losses. In particular, a short put position carries positive delta, implying that profits increase as the underlying price rises and losses accrue as it falls. During sharp market declines, this directional exposure intensifies due to negative gamma, causing losses to accelerate non-linearly. We therefore focus our analysis on delta and gamma risks, which are the primary drivers of tail losses in naked put strategies.

Delta Risks

Delta risk for a short put is straightforward to interpret. A short put position carries positive delta, meaning the option’s PnL responds directionally to changes in the underlying stock price, in this case, AAPL. As a result, the strategy benefits from rising or stable prices but incurs losses when the underlying price declines.

Since each trade is held for ~ 4 days, adverse directional moves during this window can dominate the PnL outcome, particularly during periods of heightened market stress.

However, delta risk alone assumes a linear directional exposure, whereas in reality the sensitivity of a short put position evolves dynamically as the underlying price moves, which is a result of gamma exposure.

Gamma Risks

Gamma risk arises from the fact that the delta of a short put position is not constant, but increases in magnitude as the underlying price moves. For naked puts, gamma is negative, implying that adverse price movements cause delta exposure to intensify against the trader. As the underlying price declines and the option moves further in-the-money, the effective long delta of the short put position increases rapidly.

This leads to a non-linear loss profile, where losses accelerate disproportionately during sharp or large price declines. As a result, gamma risk is the primary mechanism for tail-loss amplification, particularly over short holding periods and during stress regimes. This convex downside exposure explains the negatively skewed and fat-tailed PnL distribution observed, as well as the magnitude of the ES relative to VaR.

Conclusion

These risks give rise to the motivation to incorporate appropriate risk management measures to mitigate tail-risks, while still preserving the strategy’s ability to monetise VRP.

In the next section, we will explore of these measures.

PS: GenAI was used to support the writing of this piece - but mostly for equation writing, cleaning up of markdown formatting, and language!

AlphaSteph